This is the third part of the graph theory notes. We take a look at $k$-partite graphs and Turán’s Theorem. We omit the Tactics section since most problems can be handled by tactics mentioned earlier combined with the powerful results mentioned below. However, it might be worthwhile to see the connection of Inequalities (like - AM-GM, Cauchy-Schwartz etc) to problems related with finding bounds of edges.

The book followed throughout is: Graph Theory with Applications by Bondy J.A., Murty U.S.R.. Please refer to the book for examples as well as visual graph drawings.

$k$-partite Graphs⌗

Let $G$ be a graph with with the vertex set $V$ then if

1. The vertex set can be decomposed into a union of $k$ subsets such that any two subsets are disjoint i.e $$V = \bigcup\limits_{i = 1}^k V_i \qquad V_i \cap V_j = \phi$$ for some $i \neq j$
2. There is no edge whose two vertices are in the same subset

then if these two conditions are met, we call a graph k-partite. A 2-partite graph is called a bigraph (which are the same as previously defined term, bipartite graph). A $k$-partite graph is denoted by $G = (V_1,V_2,\dots,V_k;E)$ or $G = (V_1^k;E)$

It is not difficult to convince oneself that any graph with $n$ vertices is $n$-partite graph.

$$\dotsb$$

Suppose that $G^\prime$ is a simple $k$-partite graph as in $G^\prime = (V_1^k;E)$ with $| V_i| = m_i$, $i \in \lbrace 1,2,3, \ldots \rbrace$. The graph is said to be complete k-partite if any two vertices belonging in two different subsets of the vertex set $V^\prime$ are adjacent, i.e, $u \in V_i , v \in V_j , i \neq j$ and $u$ is adjacent to $v$. We denote the graph $G^\prime$ as $K_{m_1, m_2, \dots , m_k}$ and more frequent notation is $T_{k}(n)$ where $n$ stands for the total number of vertices.

A complete bigraph is shown below, denoted as $K_{2,3}$ or $T_3 (5)$.

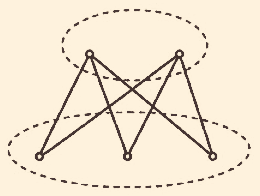
Complete bigraphs do not contain triangles made with the vertices of the graph itself.

A complete graph and a complete $k$-partite graph are $k$-regular for some $k$.

Theorems⌗

Theorem 1: If a graph $G$ with $n$ vertices contains no triangle, the largest number of edges of $G$ is $\left[\frac{n^2}{4}\right]$ where $\left [ .\right]$ represents the greatest integer function.

Hint: Prove by Induction.

$$\dotsb$$

Theorem 2 [Turán]: Suppose $G$ contains no $K_{k+1}$, then $e(G) \leqslant e(T_{k}(n))$. The equality holds if and only if $G \cong T_{k}(n)$.

Key: The $\cong$ represents ‘isomorphic’. The $e(.)$ stands for the number of edges. $G$ is any simple graph. $T_{k}(n)$ represents a complete $k$-partite graph with $n$ vertices. $K_{k+1}$ is the complete graph with $k+1$ vertices.

The proof can be found in the book Graph Theory with Applications by Bondy J.A., Murty U.S.R. as was mentioned in Part 1 of these notes.

Note 1: This theorem’s proof is not necessary for olympiads/scholarship exams. Theorem 1 is rather common and is sometimes referred to Turán’s theorem as well.

Note 2: $e(T_k(n)) = \binom{n - k}{2} + (m-1)\binom{k+1}{2}$ where $k = \lfloor \frac{n}{m} \rfloor$

$$\dotsb$$

Theorem 3: [“Marriage Lemma” or Hall’s Matching Theorem] Let $G$ be a bipartite graph with parts $A$ and $B$. Suppose that $B$ has at least as many vertices as $A$. Then $G$ has a matching using all the vertices of $A$ if and only if for any subset $S$ of $k$ vertices of $A$, there are at least $k$ vertices in $B$ adjacent to some vertex of $A$.

In particular, if every vertex of $A$ has the same degree $a$ and every vertex of $B$ has the same degree $b$, then $G$ has a matching using every vertex of $A$.

Questions⌗

1. Prove that if there are $2n+1$ vertices and $n^2 + n + 1$ edges in a simple graph $G$, then $G$ must contain a triangle.

2. $G$ is a graph with $n$ vertices and $n+1$ edges. Prove that there exists at least one vertex whose degree is no less than 3.

3. In a circular city whose radius is 6 kilometers, there are 18 police cars making the rounds. They use wireless equipments to communicate with each other. If the wireless is effective within 9 kilometers. Prove that at any time, there must exist two cars, each of them can communicate with five other cars.